A propósito de los polígonos, veamos como hace cientos de años se demostró GEOMÉTRICAMENTE y ARITMÉTICAMENTE el TEOREMA DE PITÁGORAS.
El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de los cuadrados de los catetos (los dos lados menores del triángulo, los que conforman el ángulo recto).
Si un triángulo rectángulo tiene catetos de longitudes
y 
, y la medida de la hipotenusa es 
, se establece que:
El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de los cuadrados de los catetos (los dos lados menores del triángulo, los que conforman el ángulo recto).
Si un triángulo rectángulo tiene catetos de longitudes
y , y la medida de la hipotenusa es , se establece que:(1)
De la ecuación () se deducen fácilmente 3 corolarios de aplicación práctica:
 |  |  |
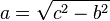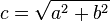Muy buena explicación, y gracias por la información dada.
ResponderEliminar